Habi Hablóg

I'm A Goofy Goober

Habi -

04/02/2012 19:25:43 -

Tecnoesoterismo

Intentaré ser poco matemático, que se me asustan los lectores.

Existe un método de construcción de fractales llamado IFS, basado en el hecho de que una aplicación contractiva tiene un punto fijo (atractor por tanto). Supongamos que trabajamos en R² y que nuestras aplicaciones serán transformaciones afines de la forma:

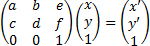
Lógicamente si a, b, c y d son menores que 1 en valor absoluto, entonces es contractiva.

Generalizando: si tenemos n transformaciones así y les asociamos una probabilidad p_i (con i entre 1 y n) a cada una tenemos el llamado “juego del caos”, en donde partiendo de un punto vamos transformándolo aleatoriamente según la regla que le corresponda. Y por la autosimilitud (puntos fijos) del sistema tenemos una bonita fractal. También representaremos cada aplicación en una línea para ahorrar (y para no tener que usar tensores).

Ejemplos:

- - -

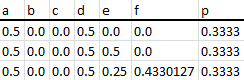
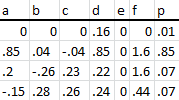
Bien. Para una de las asignaturas de libre configuración de la carrera (teoría del caos) hice un programa de fractales con varios módulos, entre ellos uno IFS. Entre otras cosas. La verdad es que las prácticas fueron una sobrada en todos los sentidos; por ejemplo, incluí ésta fractal IFS con mi nombre:

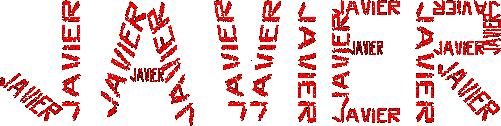
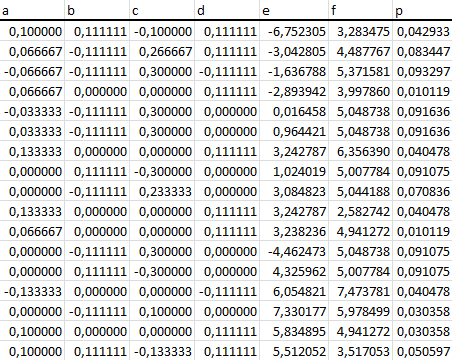
El truco es fácil: dibujamos un rectángulo en un papel, y calculamos las transformaciones que lo llevan a cada uno de los palotes que conforman cada letra; además, se puede distribuir la probabilidad en función del área de cada palote, para que el relleno de puntos sea más uniforme. En los fractales anteriores el degradado de negro a color representa la densidad de puntos en esa zona.

- - - - -

Años después, cuando terminé la carrera y para celebrarlo, decidí darle una vuelta de tuerca. Una de nuestras coñas era que al unir una colección de puntos cualquiera siempre aparecía la cara de Goofy.

Así que... cogemos una imagen de Goofy (mapa de bits 256x256 representando a [0, 1]²) y por cada pixel que pertenezca a su cara escribimos la línea de la aplicación correspondiente.

Lógicamente a_i=d_i=1/256, b_i=c_i=0, e_i=x_i/256, f_i=1-y_i/256, y p_i=1/n para i de 1 a n (n en este caso es 10.098, el número total de píxeles y por tanto filas de la matriz) y x_i e y_i son la columna y fila respectivamente del pixel en cuestión en su mapa de bits correspondiente.

En cualquier caso, ésta y no otra es la historia de la fractal de la cara de Goofy.

...

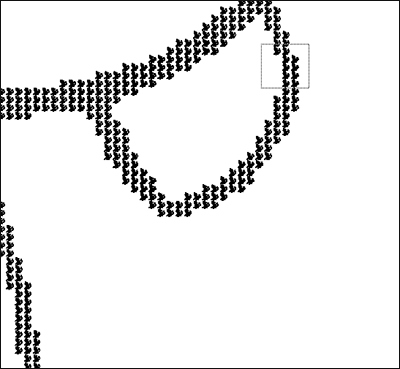
[ Celebrémoslo. ]

Jorge - 09/02/2012 15:26:10

Hola fenómeno (o tigre como diría un antiguo profe):

Quería ponerme en contacto contigo para resolver una pequeña y fácil duda sobre células de baterías portátil. Si tuvieras a bien enviarme un mail...

Aquí un nerd en electrónica, ahí un fenómeno.

Habi - 10/02/2012 20:12:49

Contestado.

L - 17/02/2012 12:35:30

¡Dios mío, era cierto! Uniendo cualquier cantidad de puntos sale Goofy. No me esperaba verlo demostrado con tanta contundencia.

Por cierto, offtopic: la fe de vida voló. Ya decía yo que me notaba muy frío. ¿Qué ha pasado?

H - 17/02/2012 22:18:29

Me temo que la fe de vida murió; o al menos dejó de dar fe de vida.

Además, siempre puedes saber si Z sigue viva mirando a su FarmVille; o en mi caso, la cuenta del Kingdom of Loathing.

Pablo - 22/03/2012 7:15:33

y si la transformacion fuese de r3 a r3?

Habi - 22/03/2012 11:01:30

Si tienes un display holográfico, adelante.

Ya más en serio, vale obviamente para cualquier R^n con las generalizaciones pertinentes (en el caso que comentas, matriz de la transformación de 4x4 y 13 columnas en la otra).

Yo lo hice en aquellas prácticas en R^3 usando cónica (definiendo a priori los parámetros de la perspectiva, dibujando el pixel transformado en cada paso) para el típico helecho y poco más, aprovechando el "engine" 3D que hice para ver los atractores.

Si quieres un Goofy tridimensional recursivo, te tocará voxelizar. El proceso es trivial (e idéntico).

Post cerrado

Acerca de

Red antisocial

Últimos posts

Últimos comentarios

Calendario

Categorías

Cenas de Abj

Frase célebre

I'm A Goofy Goober